Modelo Dinâmico de Nelson-Siegel

O modelo de Nelson-Siegel Dinâmico (DNS) é usado para estimar a curva de juros, ver Nelson & Siegel (1988) e Diebold & Li (2006) para mais detalhes.

A versão dinâmica é definida na equação abaixo:

$$ y_t(\tau)=L_t + S_t \bigg(\frac{1-e^{-\lambda\tau}}{\lambda\tau}\bigg) + C_t \bigg(\frac{1-e^{-\lambda\tau}}{\lambda\tau}-e^{-\lambda\tau}\bigg), $$

no qual:

$\tau$ é o vencimento do título (em meses),

$y_t(\tau)$ é o juro (yield) observado por vencimento e em uma determinada data,

$L_t$ é o nível (level), interpretado como fator de longo prazo,

$S_t$ é a inclinação (slope), interpretado como fator de curto prazo,

$C_t$ é a curvatura (curvature), interpretado como fator de médio prazo,

$\lambda$ é o parâmetro de decaimento.

O exemplo abaixo é baseado em um conjunto de dados bem conhecido na literatura. São dados mensais entre Janeiro/1972 a Dezembro/2000, com maturidades entre 3 e 120 meses. A seguir, vamos estimar os parâmetros do modelo e os juros. Primeiro, vamos carregar os dados.

import numpy as np
import pandas as pd
# Dados
url = "https://www.dropbox.com/s/inpnlugzkddp42q/bonds.csv?dl=1"
df = pd.read_csv(url,sep=';',index_col=0);
df.head() # Yields observados

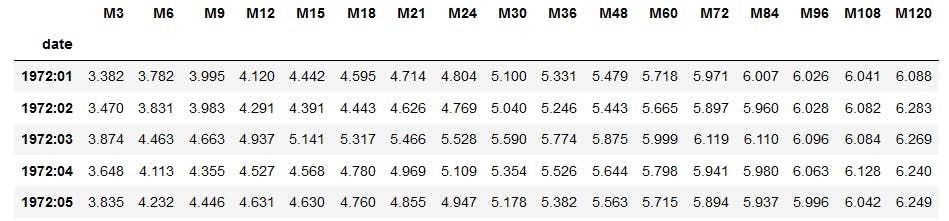
Segundo, vamos calcular a matriz de carregamento - é a matriz na qual a primeira coluna é formada por 1's, a segunda é formada por $ \frac{1-e^{-\lambda\tau}}{\lambda\tau} $ e a terceira por $ \frac{1-e^{-\lambda\tau}}{\lambda\tau}-e^{-\lambda\tau} $. Sua dimensão é $\tau \times 3$.

# Matriz de carregamento
import numpy as np
def Nelson_Siegel_factor_loadings(lam,mty):
 c1 = np.ones(mty.shape[0])
 c2 = (1-np.exp(-lam*mty))/(lam*mty)
 c3 = c2-np.exp(-lam*mty)
 lambmat = np.vstack((c1,c2,c3)).T
 return(lambmat)

l = df.shape[0]
mty = np.array([3,6,9,12,15,18,21,24,30,36,48,60,72,84,96,108,120])
T = mty.shape[0]
lam = 0.0609

Z = Nelson_Siegel_factor_loadings(lam = lam, mty = mty)

Terceiro, vamos calcular os fatores $L_t$, $S_t$ e $C_t$ e os yields.

import pandas as pd
from numpy.linalg import inv

def Yhat_betas(Y,Z):
 beta = np.matmul(inv(np.matmul(Z.T,Z)),df.dot(Z).T).T 
 Yhat = beta.dot(Z.T)
 return(beta,Yhat)

results = Yhat_betas(Y = df, Z = Z)
results[0].head() # Fatores L, S, C.

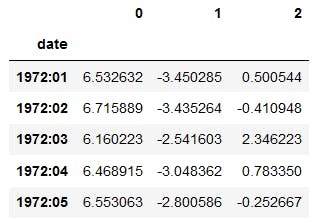
results[1].head() # Yields estimados

Agora vamos estimar os parâmetros - VAR(1) - que governam a dinâmica dos fatores $L_t$, $S_t$ e $C_t$.

# Matriz dos coeficientes do VAR(1)

def VARcoeff(betas,l):
 YY = betas.values # To convert a pandas dataframe to a numpy ndarray
 XX = np.column_stack((np.ones(betas.shape[0]),YY))
 XX = np.delete(XX,(l-1),axis=0)
 YY = np.delete(YY,0,axis=0)
 var= np.matmul(inv(np.matmul(XX.T,XX)),np.matmul(XX.T,YY)).T
 return(var)

var = VARcoeff(betas=results[0],l = l)
var[:,1:4]

A seguir, apresento as médias do $L_t$, $S_t$ e $C_t$.

np.mean(results[0])

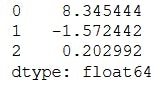
Por fim, a matriz de transição dos fatores estimados.

res = np.empty(((results[0].shape[0]-1),results[0].shape[1]))
res[:] = np.nan
for i in range(0,results[0].shape[0]-1):
 res[i,] = np.matmul(var[:,[1,2,3]],np.array(results[0])[i,]) - np.array(results[0])[i+1,]

np.cov(res.T)

Os valores dos parâmetros estimados acima são praticamente iguais aos estimados no site do Matlab relativos ao two-step approach.

Até a próxima!

Modelo Dinâmico de Nelson-Siegel

Yields e parâmetros estimados por MQO em Python